Slope Intercept Form Dice Activity!

I tweeted today about my students getting randomized practice using dice today:

Randomizing our slope intercept form practice using dice and dry erase templates! #teach180 pic.twitter.com/vLyF8ElXmA

— Liz Mastalio (@MissMastalio) October 24, 2017

I figured I would blog about the templates!

We just started our new quarter this week, and we had learned how to graph using slope intercept form before finals last quarter, but I knew students still hadn’t mastered it, then we started this quarter out learning how to write slope intercept form equations starting from a graph. I decided to make this randomized practice for a few reasons:

First, I asked the students to have me check their work after each problem before they could move on. This really let me know who was getting it and who wasn’t, and I didn’t let them move on to the other side of the template until I felt confident that they knew what they were doing on the first part! They all started with the graphing and then moved to the writing equations side.

Second, I wanted any “special cases” like vertical or horizontal lines to come up naturally when they were writing equations. We had already practiced the special cases enough in the graphing for me to feel comfortable that they were okay with those, so it wasn’t too big of a deal that you couldn’t get those cases on that template.

Third, it’s kind of fun to let the dice decide! I think students feel like this is a bit less in my control so then they tend to take even the more challenging problems in stride instead of just getting grumpy with me for assigning them a “hard one”.

Here is the “graphing” side of the template:

Notice that the differences between options 1-4 are where the negatives are. When I use this activity again, I’ll probably change #5 and #6 to be horizontal and vertical lines, so y=___ and x = ____.

Here’s the “writing equations” side of the template:

Some of these create lines with y-intercepts that don’t show on this graph window, or are non-integer values. When my students ran into these, I had them estimate where they thought they would be and let them know that there would be another strategy to deal with these that we will learn in a few weeks (we will be learning about point-slope form equation later this unit). I made the sets of A and B points so that many of them would result in integer y-intercepts and easily simplified slopes, but that some wouldn’t. This was intentional to preview the need for other types of linear equation forms.

My students who mastered both of these skills with enough time left in our class period, I asked to give me a written explanation, in words, of how you write an equation to go with a line. I’m trying to give them more practice writing in math class, communicating their ideas. They’re very reluctant to do this and aren’t very confident yet, but I got some fairly decent explanations (most were incomplete or lacking a lot of detail, but we’ll work on it!).

Download these templates in PDF form here.

Algebra 2 Unit 2 Interactive Notebooks: Solving Quadratics

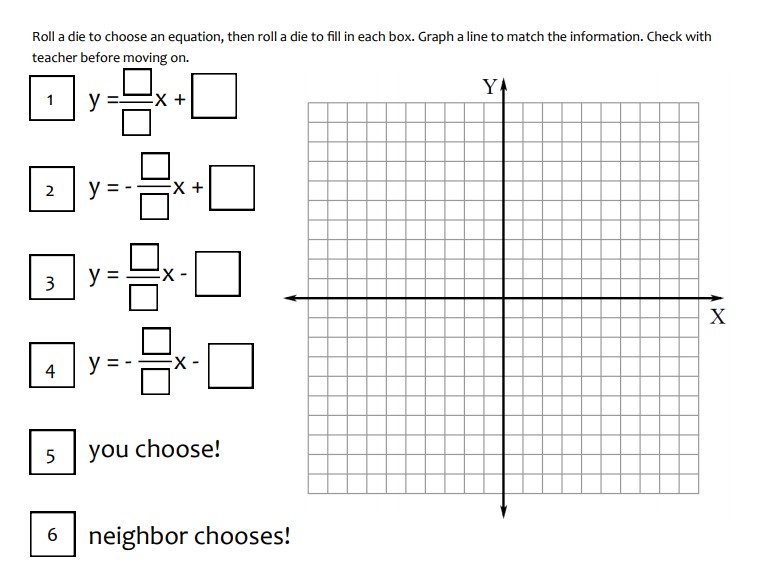
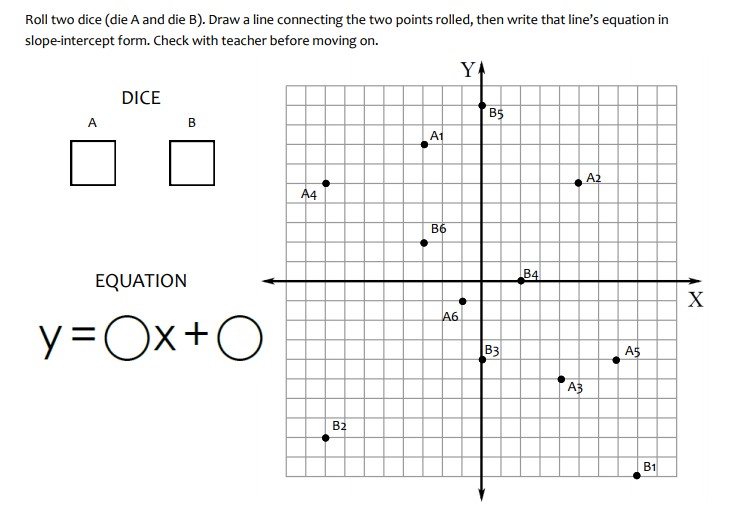
This year I’ve committed to posting each unit of both my Algebra 1 and Algebra 2 INBs.

My district is moving to a standards based curriculum, and has identified priority standards for every course. These are the standards we are required to address and assess our students over, so they pretty much form our units.

Other Algebra 2 INB Posts:

Unit 1

Algebra 1 INB Posts:

Unit 1

Unit 2 in Algebra 2 covers N.CN.C.7:

Solve quadratic equations with real coefficients that have complex solutions.

On our index page you can see the skills I broke this down into. Skills 1-4 review methods they (should have) learned in Algebra 1 to solve quadratics with REAL solutions, then we get into the complex solutions idea.

I’ve already decided that I don’t really care about my students recording their assessment scores in their INBs (mostly because I constantly forget to remind them to do this) so starting with our next standard I’m taking those boxes at the bottom off.

In this unit I found myself creating most of my INB pages from scratch (or inspired by those of other teachers), so all of these were created by me!

Skill 1: I can solve quadratic equations using inverse operations.

I wanted to emphasize WHEN you can use this method, because my Algebra 1 students continuously try to use inverse operations always when solving quadratics and force it to work even when it shouldn’t.

The poof booklet underneath the instructions has 6 example problems that we solved together, including one that cannot be solved using inverse operations to reinforce that. I think this emphasis worked really well because I did  not have a lot of students trying to use this when they shouldn’t. We’ll see if it works as well with my Algebra 1 students when they get to quadratics at the end of the year!

Skill 2: I can factor a quadratic expression and use factored form to solve solutions or graph.

So this (and inverse operations, and completing the square, and quadratic formula) is supposed to be just a review from Algebra 1. First of all, I have a lot of students who definitely never mastered this in Algebra 1. Second, they were probably taught to factor using one of the many factoring strategies that involves, at some point, guessing and checking a bit. I prefer to teach factoring using the box method, as shown in these notes. My students prefer to have something concrete that doesn’t require them to guess and check. It’s a win-win. As we practice this, I encourage them to use other factoring methods if they learned them well and prefer them, or to skip writing down steps in this method (for example, not listing out every single factor if they can mentally find the right pair immediately). They see a lot of patterns when factoring this way, I find.

I made a dry erase template for them to use when practicing this, and we discussed what parts were the most critical parts to put on paper to show their work. The template is a new iteration formed by a few years of teaching factoring this way and inspired by versions of it from a few other teachers on twitter that I’ve seen! I really like this iteration and don’t think any major changes need to be made at this point.

I gave my students the factor chart you see in the pictures, and originally did not have them put it in their notebooks. When they asked “can we just put this in our notebooks too?” I thought, “duh, why did I not do that originally?”. So next year, I’ll probably print a slightly smaller or somehow more notebook-friendly version of that chart and include it.

We began by just factoring expressions, and then in a poof book moved to solving equations by factoring. I wish I had included some quadratics that cannot be factored here, because my students later got frustrated when they ran into quadratics that I told them they could choose a method to solve, and they wanted to choose factoring…and you couldn’t factor that particular quadratic.

The graph sketching was mostly to remind them that the solutions to the quadratics were the x-intercept of the graph, but I realize now that since this isn’t really the focus of this particular standard, I could have left that whole bit out and moved it to when we talk about polynomials later this year. The poof book itself was good, but it just isn’t necessary in this standard and we could  have had more practice time! (which we were short on at the end of this quarter)

Skill 3: I can solve quadratics by completing the square.

This is also supposed to be covered in Algebra 1, but it is the skill that most often gets cut at the end of the year due to time. If they can solve quadratics other ways, and you need to fit in that last unit…completing the square goes. So this was new to most of them.

We started by going back to algebra tiles, because I think this really reinforces two things about completing the square: first, the SQUARE that we are actually completing and second, the splitting the x term in half to form said square. We didn’t actually solve these all the way through, just got them to a point where they looked like inverse operations problems to see the setup. We did a few other examples as a class that they didn’t write down and talked about patterns like the splitting the x term and the fact that you always end up adding positive ones tiles.

I made another template to help us complete the square using algebra, but this one is at a not-so-final iteration stage. My students ended up struggling most with two things. 1. factoring out A – they always forgot to actually factor it OUT of the B term. I would like to somehow emphasize this more by giving them room to show the division on the template or something. 2. multiplying what they added by A before adding it back on to the other side. I put this in small print, so maybe just making it bigger would help. Otherwise, this is the best completing the square has gone for my students in my teaching history. I’m looking forward to making some small changes here and seeing how my Algebra 1 students get on with it later this year.

Skill 4: I can use the Quadratic Formula to find solutions to quadratics.

I am realizing as I type this post that I was really inconsistent with the wording of all these skills…I like this wording better than “solve quadratics using…” so NOTE TO SELF to change all of those to be the same for next year.

I made a dry erase template for this as well, but after realizing that I would pretty much want my students to write all of it on paper to show me their work, I didn’t think there was much point to using them. So we used it as a structure to take notes on, but then didn’t use the templates when practicing. I would like to make an actual box to write about what the discriminant means next time instead of just writing it in the corner, but the students did really well with this. None of them struggled with finding B squared with a negative B value, either, so our note about using parentheses must have helped!

I wish I would have made sure there was an example here with a discriminant of 0. A negative discriminant might have been nice to see as well, although we address those after we learn about complex numbers, just to put in our notes “to be continued in a few days” or something, to get them curious about the square root of a negative number. However, some of them ran into this when they did their practice, because they calculated their discriminants incorrectly and then were trying to take square roots of negative numbers on their calculators.

Skill 5: I can do math with complex numbers and find complex solutions to quadratics.

We introduced this skill by sharing the experiences students had during the last practice when they got a negative discriminant, and then watched this video to introduce imaginary numbers.

We then did some basic math with i to see how its powers form a cycle. Students thought this was pretty wild, that it went from imaginary to real and back again! We used the square roots on the right side of the table to talk about what to actually do with i for our purposes of solving quadratics. There should have also been a lesson in here about simplifying radicals, but we ran out of time, so we left the radicals as is unless it came out to a whole number. I’m hoping we can get to that skill when we address solutions to polynomials 2nd semester – there’s a lot more time scheduled in for that standard than this one!

Then, we just did some examples. Most of them have no real solutions, but a few of them had real solutions just to show students that they need to be able to identify when to use i.

I wish that we had not solved all of these using the Quadratic Formula, because when my students were trying to solve using different methods and came upon the square root of a negative number, they somehow thought it was different than this! I could have used the same examples and just solved one by completing the square instead.

Skill 6: I can select an efficient and appropriate solution method for any quadratic.

Students were pretty easily able to fill in which method went where at the bottom of this flow chart. Again, we were running out of time in the quarter (my students this year really did not act like the solution methods to quadratics were review, so we needed to spend a lot of time on them) and if we had more time, I would have done a card sort and discussion with students sorting various quadratics by the method they would use to solve them WITHOUT actually solving them. It also would have been cool to have students race to solve the same quadratic using different methods and discuss that.

My students were mostly able to settle on one or two methods they felt most comfortable with, and realize that they needed to be able to feel comfortable with either the Quadratic Formula or completing the square to be able to solve ANY quadratic, but they definitely were not choosing the most efficient methods each time. However, this little discussion did help them to know when certain methods wouldn’t work and give them a bit of insight into how to save themselves time.

You can find all the resources shown in this post HERE, most of them in both PDF and Publisher (or Word) format.

Put Down the Pencil

Something one of my professors in college told me, and something I read again in someone’s tweet or blog post recently (cannot remember where…) is that the teacher should never be the one holding the pen(cil) when helping a student with independent work.

When helping a student, the STUDENT should be the one doing all the writing. It’s so tempting to grab their pencil, or unclip my own pen from my lanyard, or grab the dry erase marker at their table, and write for them as I walk them through the problem. But what do they get from this? They’ll be at the same point they probably were before: “It makes sense when you do it at the board, I just can’t do it myself!”

I’ve been trying so hard in the last week to put down the pencil. To instruct them what to write, point to where they should write it, but NOT WRITE IT MYSELF. It’s hard. Students move SO SLOWLY sometimes and you just want to finish up so you can go help the other 3 students raising their hands. Yes, it would be easier to write it myself, even upside down. NO, that is not what is best for my student’s learning.

I have not been 100% successful here. It’s especially hard for me when I literally point to the exact spot where a student should write a number and then they inexplicably DON’T PUT THE NUMBER IN THAT SPOT.

My strategy for when I absolutely cannot make myself leave the pencil down is to grab the dry erase marker and write them out a SIMILAR example, but still make them write the one we were working on themselves.

I can tell this is going to be a long process. But I think it’s worthwhile, and I’m going to work hard at it. I’ve found myself with my pen in hand this week, halfway through writing something on a student’s paper and thought “shoot! I’m holding the pen!”

Students holding pencils. Students writing math. That’s my goal. I’m working on it.

Eternal Newness

It’s my fifth year teaching this year, and I guess some part of me wildly thought that I would be starting to get “on top of things”. Instead I feel like Sisyphus, eternally pushing the boulder up the hill.

Sometimes I feel like this because it is so stressful. We have what feels like 17 new initiatives in my building/district this year, from standards based grading pilots to PBIS implementation. I’m teaching a new course that has only been taught once before in district and is now co-taught when it wasn’t previously. I started grad school this summer and am trying to adapt my life to be able to work and be a student at the same time. (I’m currently procrastinating on my statistics homework by writing this post, so you judge for yourself how well that balance is going).

Yet, sometimes I feel like this because it is so delightfully new. Rebecka Peterson’s post this week really resonated with me.

I love that I have a job I’ll never master. I love that there will always be room to grow. I love that there’s never an excuse for boredom in this field.

I love that every year, I get a new group of students. It’s like a puzzle to figure them out – what motivates them? What are their prior successes in math (usually very few or none)? What do they dream for themselves? How can I break down their walls?

It’s at this point of the year that I’m finally starting to figure that part out. I’m building the relationships with my students that I so treasure, the ones that literally make me get up in the morning to go fight a war for these kids – a war that some people don’t recognize as a war because my battles come in the form of helping them understand math, helping them find academic success so they can achieve whatever they want to achieve.

The relationships are a double edged sword too, though. After the shooting in Las Vegas, my kids came to school and spoke with fear about how many guns the shooter legally had. They note that their uncle, their cousin, their dad also legally has n assault rifles, pistols, machine guns in their home. They wonder how we can be ready if it happens in our halls. They wonder how they can be safe.

As I get to know them, they open up to me. They tell me of the anxiety they feel, the intrusive thoughts, the terrible words spoken to them by parents, by bosses, by other teachers even (hopefully, hopefully never in our building). They describe their parents in jail, the drug use in their homes, the need for them to take care of siblings or their own children with little help. How they have to work from 4-11 after school to support themselves or their family and don’t get home until after midnight, just to wake up before 6 to catch the bus to school.

Rebecka goes on in her post to describe how incredibly hard teaching is, and I’ve had the realization this school year so far that it is never going to get easier. There’s never going to be a point in my teaching career where I don’t have to work incredibly hard. I will never be “on top of things”, which is super hard for my logical, organized, need-to-know-all-information-possible Ravenclaw personality to handle. I know I will always want to tailor my lessons from last year to fit this precious and incredible group of students that I have this year. I will always want to adjust my grading practices, to stay after school and have discussions with my office mate about the best ways to give them feedback, the best ways to give them second chances to show understanding.

I will always build relationships with my students that lead them to sharing the horrors of their young lives with me. I will continue to hear about experiences that I could never imagine dealing with at my own age of 27 (or older, as I continue to widen the age gap between myself and my students) but that they have had to deal with at 16, at 12, their whole lives. I will lie awake at night thinking helplessly about how I can find a way to provide the girl in my second period with some clothes, or food. About how I can make sure the girl in my Algebra class has the right support around her when her baby is born. About the boy who shared with me his suicidal thoughts, and the fear I feel every time he hears bad news, that he will react by giving in to those thoughts. I will continue to bear the burdens of my hundreds of students, how they fear going to a party, even just a bonfire at someone’s home, and never returning because someone showed up with a gun.

It is such a hard job. Those who think that teachers have it easy are delusional, and I am not afraid of using language that strong. They fail to understand that while our contracts are from 7:30 – 3:30, Monday-Friday, August-May, the job follows us everywhere. It’s with us at home when we’re grading or preparing lessons for next week (my students express concern when their gradebook app gives them notifications at 10 pm on a Friday). It’s with us when we check twitter and see news of another shooting in town, hearts beating and hoping against hope that when we open the article it’s not one of our kids. It’s there when we stay in a hotel and grab all the toiletries before we leave to bring to school for students who can’t afford them. It’s there in pride as well, when we run into former students at the grocery store or at the bar where they work, students who tell you how their college classes are going, the job they just got. When you listen to an entire album of  band you’ve never heard of because one of your students is so excited to go to their concert. When you think of the inside joke with your Algebra 2 class about you being a vampire who’s really 217 years old.

Teaching has all the highs and all the lows. It is always, always worth it, but sometimes it is so, so hard.

This week was one of the hard ones. Then, at the end of the week, our English department decided to participate in Alicia Keys’ #wearehere campaign. I found myself sobbing on my couch on a Friday night looking at all of the hopes and dreams of my students. Their courage, their relentless perseverance, their positivity through it all are what bring me back in every time I have a day where I think, “wow, think about how easy having an office job could be.”

Edit: You can view the students’ video here.

But how boring. How could you ever want anything else but the crazy, intense, 24/7 rollercoaster that we have. How could you not take Sisyphus’ boulder willingly on your shoulders and push it up the nearest incline for your students on a daily basis?